Fourier Transform | Carl's Webpage

Definition

The Fourier transform in continuous-time:

$$X(j\omega)=\int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt$$

The Fourier transform in discrete-time:

$$X(e^{j\omega})=\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n}$$

$X(j\omega)$ is the correlation of $x(t)$ with $e^{j\omega t}=cos(\omega t)+jsin(\omega t)$, and $X(e^{j\omega})$ is the correlation of $x[t]$ with $e^{j\omega n}=cos(\omega n)+jsin(\omega n)$.

The Fourier transform of a time signal is its correlation to a complex sinusoid with frequency $\omega$.

$X(j\omega)$ is generally not periodic, and $X(e^{j\omega})$ is periodic with period $2\pi$.

Dirichlet conditions for $X(j\omega)$:

$\int_{-\infty}^{\infty}|x(t)|dt$ is finite.
Jumps in $x(t)$ are finite and there are a finite number of jumps in a finite time interval
There are a finite number of minima and maxima in a finite time internal.

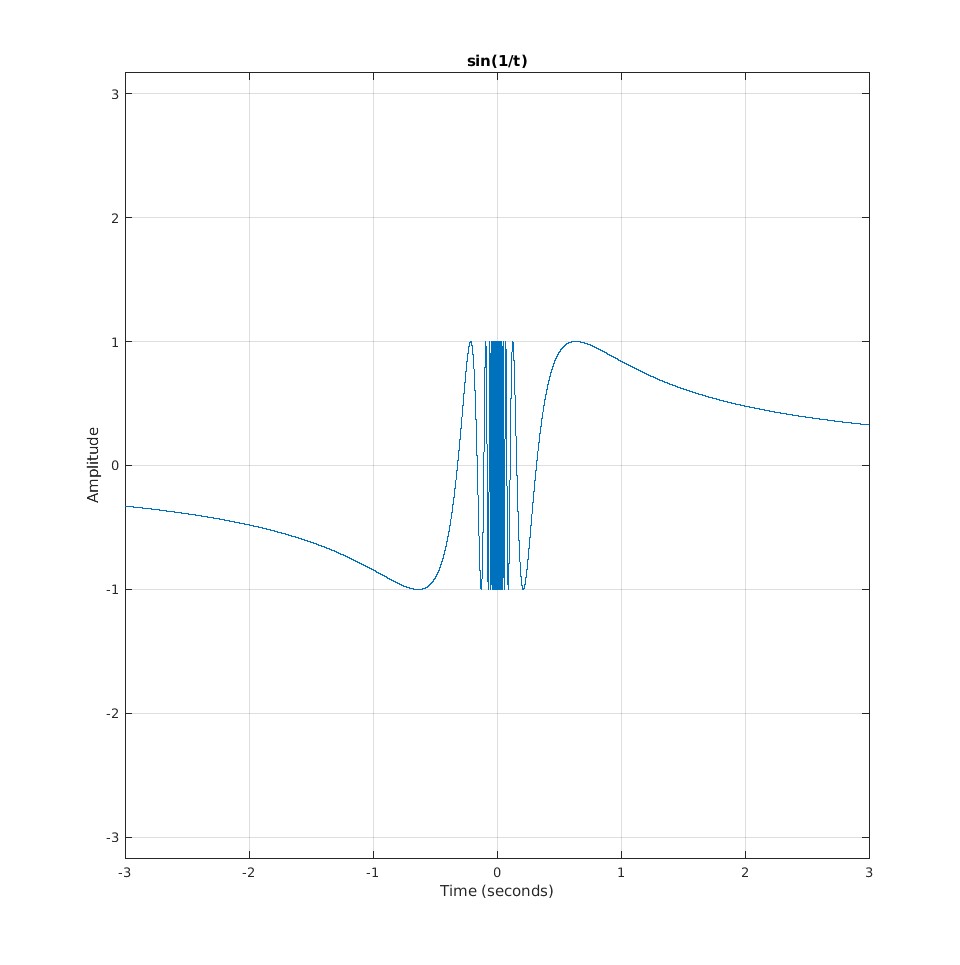
Example: $sin(\frac{1}{t})$ has infinite minima and maxima in the finite interval about the origin, so its Fourier transform does not exist:

sin (1/t)

Dirichlet condition for $X(e^{j\omega})$:

Any signal that can be physically produced in a lab satisfies these Dirichlet conditions.

$x[n]$	Condition	$X(e^{j\omega})$
$\delta[n]$	-	1
$rect[\frac{n}{2m+1}]$	$m\gt 0$	$\frac{sin(\frac{(2m+1)\omega}{2})}{sin(\frac{\omega}{2})}$
$a^{n}u[n]$	$-1\lt a\lt1$	$\frac{1}{1-ae^{-j\omega}}$
1	-	$2\pi \hat{\delta_{2\pi}}(\omega)$
$\frac{1}{\pi n}sin(\frac{an}{2})$	$0 \lt a \le 2\pi$	$\hat{rect_{2\pi}}\frac{w}{a}$

Signals and Systems

\(x[n]\)	Condition	\(X(e^{j\omega})\)
\(\delta[n]\)	-	1
\(rect[\frac{n}{2m+1}]\)	\(m\gt 0\)	\(\frac{sin(\frac{(2m+1)\omega}{2})}{sin(\frac{\omega}{2})}\)
\(a^{n}u[n]\)	\(-1\lt a\lt1\)	\(\frac{1}{1-ae^{-j\omega}}\)
1	-	\(2\pi \hat{\delta_{2\pi}}(\omega)\)
\(\frac{1}{\pi n}sin(\frac{an}{2})\)	\(0 \lt a \le 2\pi\)	\(\hat{rect_{2\pi}}\frac{w}{a}\)